GSM receiver blocks: timing synchronization (part 3: less talk, more fight)

In the last post, we had thought up of some ideas for how to do timing synchronization. We note that this is not exactly how GSM works – with GSM you have special bursts that are used for timing synchronization, and the receiver uses those to keep its clock in sync with the transmitter. Since we’re not actually implementing a GSM receiver (how many GSM networks remain?), we’re going to look at the generic case of doing timing synchronization with a known training sequence in the presence of severe multipath (mostly for training purposes. I think this stuff is neat and I want to get better at it).

More samples, better peak, less sidelobes #

We try out various correlations and see what happens (literally, we’re eyeballing stuff here):

tiledlayout(2,2)
nexttile
[c, lagz] = xcorr(received, modulated_training_sequence(1:end)); plot(abs(c(200:end)))
title("correlation with full training sequence")
nexttile
[c, lagz] = xcorr(received, modulated_training_sequence(9:end)); plot(abs(c(200:end)))
title("correlation with TS(9:end)")
nexttile
[c, lagz] = xcorr(received, modulated_training_sequence(1:end-8)); plot(abs(c(200:end)))
title("correlation with TS(1:end-8)")
nexttile
[c, lagz] = xcorr(received, modulated_training_sequence(9:end-8)); plot(abs(c(200:end)))
title("correlation with TS(9:end-8)")
copygraphics(gcf)

and we get the following plot. Note that the vertical scale is different for each of the subplots.

OK, so as we kinda suspected in the previous post, using a longer correlation template leads to less sidelobe amplitude without obvious widening of the true correlation peak.

Writing an estimator #

Now that we’ve decided to use the full training sequence for doing correlation in time, let’s write out an estimator. First of all, we correlate the received signal with the training sequence:

correlation_output = conv(signal, conj(flip(modulated_training_sequence)));
[val, uncorrected_offset] = max(correlation_output);

Running it #

We use the same channel (otherwise the shape of the correlation peak will be different across runs), and we run it a bunch of times with the same training sequence and random data:

% signal creation
training_sequence = randi([0 1], 32,1) %[0,1,0,0,0,1,1,1,1,0,1,1,0,1,0,0,0,1,0,0,0,1,1,1,1,0]';

% channel creation
nominal_sample_rate = 1e6 * (13/48);
signal_channel = stdchan("gsmEQx6", nominal_sample_rate, 0);

modulated_training_sequence = minimal_modulation(training_sequence);

average_convolution = zeros(319,1);

average_convolution_energy = zeros(319,1);

for i = 1:1024
	data = [randi([0 1],128,1); training_sequence; randi([0 1], 128,1)];
	modulated = minimal_modulation(data);
	signal_channel(complex(zeros(30,1)));
	received = signal_channel(modulated);
	awgned = awgn(received,80);
    first_convolution = conv(awgned, conj(flip(modulated_training_sequence)));
    average_convolution_energy = average_convolution_energy + abs(first_convolution);
    average_convolution = average_convolution + first_convolution;
end

figure;
plot(abs(average_convolution));
title("average convolution output");
figure; 
plot(abs(average_convolution_energy));
title("average convolution energy output");



function not_really_filtered = minimal_modulation(data) 
	not_really_filtered = pammod(data,2);
end

Output from a single run looks like this:

And on average, we get something like this: the first image is the average of the outputs, the second image is the average of the energy of the outputs:

Eyeball-based analysis #

We observe two things:

1. There isn’t a single sharp correlation peak – it has lots of structure, even when averaged over 1024 runs. Even more disquieting, the structure seems constant across runs on the same channel, even though the data is random.

2. For a single run, there’s a lot of sidelobe energy. It gets averaged away over many runs, but our estimator needs to work on a single run only.

Don’t worry too much about the sidelobes #

In an actual system, we almost always have additional information about our signal:

• when the signal started (energy detector)
• when we expect it to start (local timing reference)
• where the training sequence lives in the signal (hopefully the implementer has read the standard)

Even if this information is somewhat coarse/inaccurate, it lets us remove some of the irrelevant bits (or rather, samples,) of the received signal before feeding it to the timing estimator, which will reduce how many sidelobes appear.

If the sidelobes are sufficiently far away from the main peak such that we can ignore them without too much additional information about signal structure, what truly matters is the shape and position of the intended correlation peak, and what’s immediately around it.

Channel shape influences correlation peak structure #

Even if we avoid the sidelobes, it’s unclear which part of the correlation peak we should use as our timing estimate. The highest peak? The first peak above a significant threshold? It’s not unambiguous.

Training/synchronization sequences are generally selected to have negligible autocorrelation at non-zero delays – to improve, well, correlating against them. This means that when we correlate the received signal against the training sequence, we’ll get something that looks like the channel impulse response estimate – and the “sharper” the autocorrelation of the training sequence, the better that channel impulse response estimate will be.

If you think of the channel as a tapped delay line, then the peak of the correlation output corresponds to the “tap” (delay) with the highest magnitude. This doesn’t necessarily correspond to the first/“earliest” tap with a significant coefficient, nor does it generally correspond to the best timing for the least-squares channel estimation.

Naturally, if we only have a single big tap in our channel, this is probably fine: as long as the single big tap is in the window for the least-squares, we’re home free. However, if we have multiple significant taps – especially if they aren’t all bunched together – and want to do a good job, things get more complicated.

We need a better way to process this hedgehog-looking correlation peak.

Sliding energy window heuristic #

Morally, to minimize bit error, we want to find the channel taps that give us the most energy. The more energy, the less the noise can perturb your decisions – that’s the extreme tl;dr of the whole Shannon thing. You don’t care about super-attenuated paths (their contributions are barely distinguishable from noise), and if you have a single path that’s much stronger than the others, you can ignore the others to pretend you don’t have a dispersive channel at all!

With Viterbi detection it’s a tad nontrivial to reason about it, but imagine a rake receiver: if you want to get the most signal energy into your decision device, you need to identify the channel taps with the most energy. The rake receiver can pick out a finite but arbitrary set of paths, but with Viterbi, we need to decide on a window of the channel to use – everything within that window gets used, nothing outside gets used. That window tends to be fairly small: trellis-based detection is a controlled combinatorial explosion.

Since that window is precious, we need to cram as much energy into it as possible, and this is precisely why the timing estimator matters here. If our timing is suboptimal, we’re dropping valuable signal energy on the floor. This inspires a timing estimator design: run a window of appropriate size over the coarse channel impulse response (which is generated by the correlation we previously looked at) and pick the offset with the highest total energy in that window.

Aside: timing error in the non-ISI case #

Note that with a more usual non-ISI case, timing matters because we want to sample the signal at the best time, otherwise the eye diagram closes and we get more bit errors. In this receiver architecture, channel estimation + Viterbi take care of that consideration: the fine timing estimate is, in effect, “baked into” the channel estimate.

Creating the estimator #

To find the size of the window, we ask whoever designed our channel estimator / trellis detector what’s the biggest channel they can handle, which as usual, we call \(L\). Here, we’ve decided \(L=8\). Mathematically, we’re taking the absolute value of the first convolution, and convolving that with an \(L\)-long vector \([1,\cdots,1]\):

first_convolution = conv(signal, conj(flip(template)));
second_convolution = conv(abs(first_convolution), ones(1,8));

[val, uncorrected_offset] = max(second_convolution);

Note the abs(first_convolution). This is critical, and omitting it caused me a lot of sadness and confusion. We want the total energy in that window, and if there’s cancellation across channel coefficients/taps then we’re…not getting a total energy.

If we change our code:

average_second_convolution = zeros(326,1);
% ...
    second_convolution = conv(abs(first_convolution), ones(1,8));
    average_second_convolution = average_second_convolution + second_convolution;
% ...
plot(abs(average_second_convolution));
title("average second convolution output");

We get something that looks remarkably better. While a single run looks like this:

This looks pretty bad sidelobe-wise, but sidelobes don’t doom us.

When we average over multiple runs (which effectively “averages out” the sidelobes), we see that our new correlation erased the structure in our correlation peak. Note that it’s not the averaging over multiple runs that’s done this!

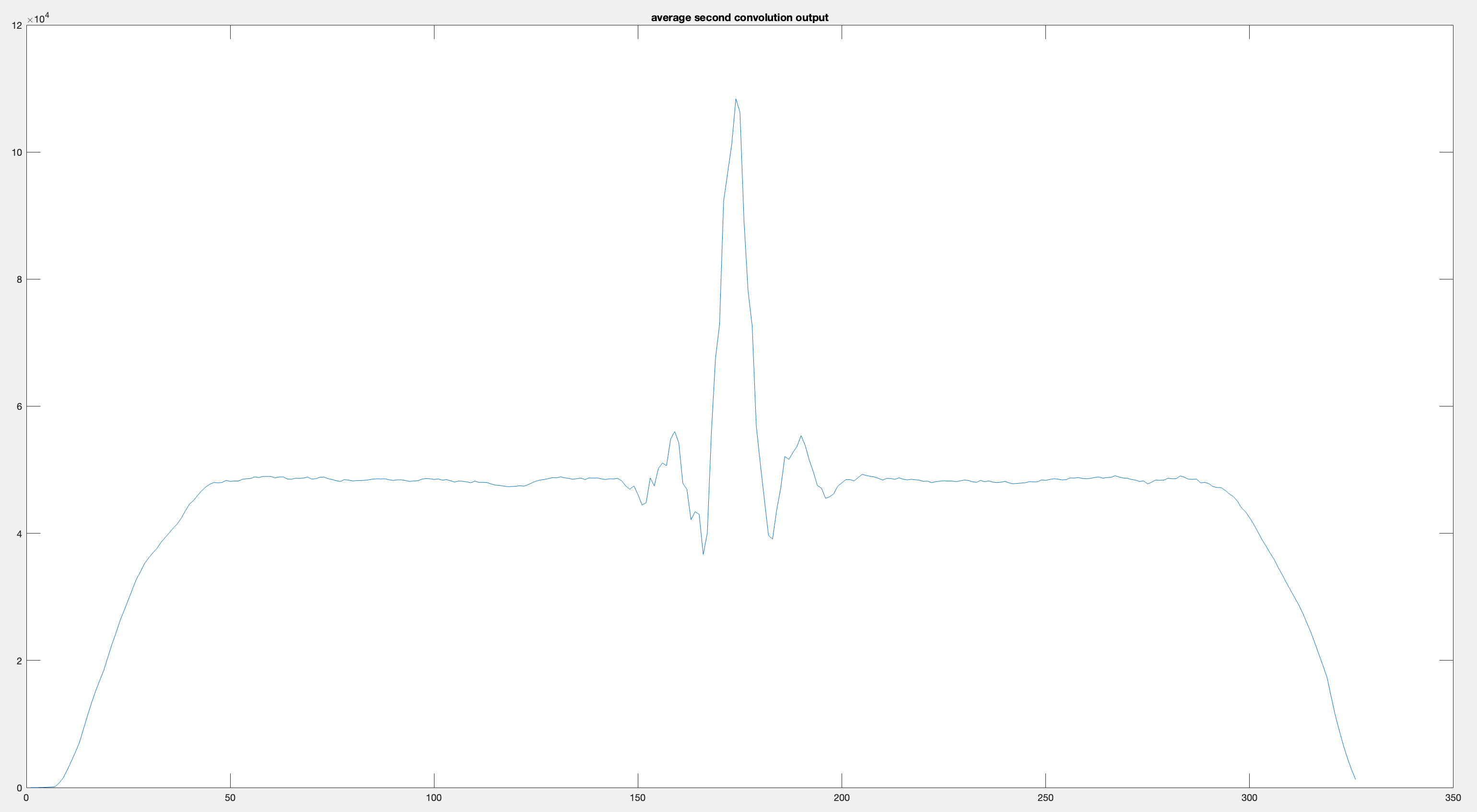
Sometimes a little structure does show up, but it’s not nearly as bad as before:

We try it with a different channel (gsmTUx12c1) to make sure that it’s not a peculiarity of the channel model we had been using:

Validation #

Convolving once against the training sequence, calculating the energy, then convolving again with a largest-supported-channel-length vector of ones certainly generates extremely aesthetic plots, but we’ve yet to make sure that it actually matches up against the ground truth.

Without any subtlety, we simply generate a loss vector (how much least-square loss for each offset) for each run, sum them all up, and plot them alongside the second convolution output:

average_ts_losses = zeros(1,264);

% ...
    ts_losses = least_squares_offset(awgned, training_sequence);
    average_ts_losses = average_ts_losses + ts_losses;
% ...

average_second_convolution = average_second_convolution / norm(average_second_convolution);
average_ts_losses = average_ts_losses / norm(average_ts_losses);

figure;
plot(abs(average_second_convolution));
hold on;
plot(average_ts_losses);
title("peak = second convolution, dip = least squares loss");

And the comparison is incredibly encouraging. Note that these are averages, so the sidelobes from the data get averaged away. We see that the convolution-based estimator has more sidelobes, but the main peak is sharp:

To show it’s not a fluke, we show a comparison for a single run:

There’s still the eternal question of the indices, which decidedly do not line up. We investigate:

correlation_indices = [];
least_squares_indices = [];

% ...
    [val, correlation_index] = max(second_convolution);
    correlation_indices = [correlation_indices correlation_index];
    [val, least_squares_index] = min(ts_losses);
    least_squares_indices = [least_squares_indices least_squares_index];
% ...

And in the command window we run:

>> sum(least_squares_indices-correlation_indices)/length(least_squares_indices)

ans =

  -29.9922

>> 

The almost-integral offset does seem to be a fluke, but we run it a few more times and see it’s not – it seems to vary a little bit:

>> clear; average_convolution_output

ans =

  -33.7109

>> clear; average_convolution_output

ans =

  -29.7305

>> clear; average_convolution_output

ans =

  -27.7578

>> clear; average_convolution_output

ans =

  -30.9141

>> 

The \(\sim30\)-ness was a bit concerning, since the GSM training sequence is \(26\) syms long and our channel/window is \(8\) long and there’s no obvious and morally-upstanding way to get \(\sim30\) out of that, but looking at our source code we see that we indeed did choose a \(32\)-long training sequence (the % is the comment character in MATLAB):

training_sequence = randi([0 1], 32,1); %[0,1,0,0,0,1,1,1,1,0,1,1,0,1,0,0,0,1,0,0,0,1,1,1,1,0]';

Residual processing #

We seem to have a little error between the least-squares timing estimator (which we’re using as a reference) and our two-correlation-based estimator, which is a bit concerning. We try to figure out what’s going on, and we start off simple:

>> min(least_squares_indices)-max(least_squares_indices)

ans =

     0

>> least_squares_indices(1)

ans =

   142

>> 

We notice that the least-squares estimator always gives the same index (\(142\)), so whatever is going on, it’s in the correlation-based estimator, and uh, there’s definitely something going on:

>> hold on
>> plot(least_squares_indices)
>> plot(correlation_indices)

That outlier is what’s skewing the average! While our code didn’t save the raw data for each run (only the outputs of the estimators), it’s clear what happened: most of the time, this estimator doesn’t get tricked by the sidelobes, but when it does, it gets tricked hard.

We plot a histogram of the indices:

>> histogram(correlation_indices, 'BinMethod', 'integers')

The most common (by far) value is \(174\), which indeed is \(142+32\):

>> 174-32

ans =

   142

>> least_squares_indices(1) % remember least_squares_indices(n)=142 for all n

ans =

   142

>> 

Noise #

We have not tested this estimator in the presence of noise. Not to sound like a excerpt from a statistical signal processing textbook, but it is essential to test how good your estimators perform in the presence of noise. Graphs with \(E_{b}/N_{0}\) on the x-axis are, strictly speaking, optional, but they do look very nice.

We won’t do a full examination of how these estimators work in noise, but we’ll take a quick look.

I ran the same code, except modified with awgned = awgn(received,4);. This adds AWGN such that the signal to noise ratio is \(4\text{dB}\). From cursory inspection of the plot below, we see that both estimators (the correlation-based one more so than the LS one) are more likely to be tricked by sidelobes in higher-noise conditions. Even if we ignore the sidelobe-caused indices, we see some variation/wobble and not a straight line. This represents error which won’t be eliminated by running the estimators on a smaller section of the signal.

Here’s the histograms for the two indices. We definitely see that the huge errors are from sidelobes and not from the correlation peak spreading out because of noise:

If we zoom in to eliminate the sidelobes, we see that the correlation peaks indeed spread out, but approximately the same amount for both estimators:

Conclusion #

The least-squares timing estimator we had been using as a reference is excellent, but it’s incredibly compute-intensive. Here, we derived and tested an alternate correlation-based estimator which only requires a convolution, a squaring operation, and a second convolution – and the second convolution doesn’t even require any multiplies!

To reduce computational effort and avoid getting tricked by sidelobes, if at all practical, we should use a priori information (a fancy way of saying “when we started receiving it” and/or “when we expect to receive it” alongside “where the training sequence lives in the signal”) about the signal to slice a section of the signal and only run the estimator on that section.

While previously we had wanted to concoct a measure for the “goodness” of a timing estimator that’d make sense for this context (trellis-based detection in an ISI channel, we’ll be looking at Viterbi itself in the next few posts.

Why try and fake it when we’ll learn and use the real thing?